Jak zmiany rynkowe wpływają na kurs obligacji?

30 kwietnia 2015
Na rynku obligacji Catalyst ceny instrumentów dłużnych są podawane jako procentowe ujęcie wartości nominalnej obligacji – jest to tzw. kurs obligacji. Jakie są zależności pomiędzy rynkową ceną danego instrumentu a jego rentownością? Czy wahania cen obligacji zawsze są takie same i czy zawsze cena niższa od nominalnej musi oznaczać złą sytuację w spółce? Na te pytania odpowiemy w niniejszym artykule. Zapraszamy do lektury.

Rentowność obligacji to inaczej jej stopa dochodu w okresie do wykupu obligacji – w praktyce stosuje się najczęściej oznaczenie Yield To Maturity (YTM) obligacji. Rentowność jest obliczana przy założeniu, że inwestor kupi obligację po cenie rynkowej oraz przetrzyma ją do terminu jej zapadalności, natomiast odsetki otrzymane z jej tytułu zainwestuje po stopie dochodu równej YTM. Stopa dochodu zmienia się w zależności od dwóch głównych czynników, którymi jest poziom ryzyka kredytowego (wypłacalności emitenta) oraz poziomu rynkowych stóp procentowych.
Ustalmy podstawowe zależności w relacji pomiędzy ceną obligacji (P) oraz jej rentownością (YTM). Dla ułatwienia w artykule rozpatrujemy obligacje o stałym oprocentowaniu. Zależności te można rozpatrywać dwojako:
  • jak cena obligacji zależy od wymaganej stopy dochodu (YTM);
  • jak stopa dochodu (YTM) w okresie do wykupu obligacji zależy od rynkowej ceny obligacji.
Wzrost stopy dochodu powoduje spadek ceny obligacji, natomiast spadek stopy dochodu powoduje wzrost ceny obligacji. Najłatwiej zaobserwować obie zależności na poniższym wykresie. 

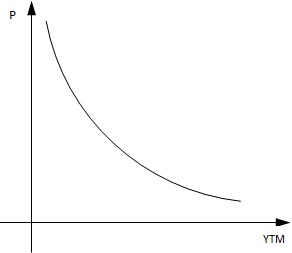
wykres 1

Omówmy wymienione zależności na prostym przykładzie.

Przykład 1
Rozpatrujemy obligacje, których termin wykupu przypada za 3 lata, ich wartość nominalna wynosi 1000 zł, oprocentowanie jest równe 6%, a odsetki wypłacane są raz w roku. Jak zmieni się cena tych obligacji, jeżeli w związku ze zmianami rynkowymi zmieni się oczekiwana stopa dochodu przez inwestorów (YTM) i wyniesie odpowiednio 5%, 6% oraz 7%?

Wzór ogólny wygląda następująco:
wzór ogólny

gdzie:
P – Cena (wartość) obligacji
Ct – przepływy pieniężne z tytułu obligacji w okresie t
YTM – stopa dochodu obligacji

  1. dla YTM = 5%
    wzór 1

  2. dla YTM = 6%
    wzór 2

  3. dla YTM = 7%
    wzór 3

Z obliczeń wynika jasno, że w przypadku gdy stopa dochodu wymagana przez inwestorów jest równa oprocentowaniu obligacji, to jej cena będzie równa wartości nominalnej (b). Z kolei gdy stopa dochodu jest niższa niż oprocentowanie obligacji (a), oznacza to, że obligacja generuje wyższe odsetki niż wynikające z oczekiwanej rentowności, a zatem jest interesująca dla inwestorów. W związku z dużym zainteresowaniem takimi obligacjami, wzrasta na nie popyt, a tym samym cena obligacji rośnie powyżej wartości nominalnej. Jeśli zaś stopa dochodu jest wyższa (c), niż oprocentowanie obligacji – inwestorzy otrzymują niższe odsetki niż oczekują z danego papieru. Wtedy obligacja jest wyprzedawana przez inwestorów, a w związku z rosnącą podażą, jej cena spada i jest sprzedawana z dyskontem (poniżej wartości nominalnej).

Z powyższego przykładu można wysnuć jeszcze jedną istotną właściwość wynikającą z zależności pomiędzy ceną obligacji oraz jej rentownością. Mianowicie wzrost wartości obligacji, wywołany spadkiem stopy dochodu o 1 pkt procentowy (a) jest wyższy niż spadek wartości obligacji wywołany wzrostem stopy dochodu o 1 pkt procentowy (c). Jak wynika z powyższego przykładu w przypadku a) cena wzrosła o 27,28, podczas gdy w przypadku c) cena obligacji spadła o 26,25.

Opisana powyżej właściwość obligacji jest nazywana wypukłością obligacji (convexity) i została przedstawiona na poniższym wykresie.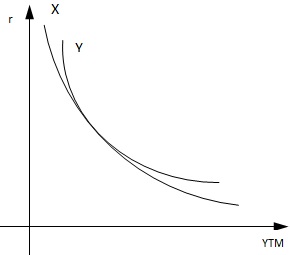

wykres 2

Obligacja Y charakteryzuje się większą wypukłością niż obligacja Y. Oznacza to, że przy takim samym wzroście rentowności obligacji, cena obligacji Y spadnie w mniejszym stopniu niż cena obligacji X. Natomiast w przypadku spadku rentowności obligacji, cena obligacji Y wzrośnie bardziej niż cena obligacji X.

Z wypukłością obligacji związane są jeszcze dwie inne, równie ważne z punktu widzenia inwestorów, właściwości:

  • im niższe jest oprocentowanie obligacji, tym większe odnotowuje się wahania cen obligacji przy zmianie rentowności obligacji (przy założeniu, że są to obligacje o stałym oprocentowaniu, jednakowym terminie wykupu oraz jednakowej rentowności na początku);
  • im dłuższy okres do wykupu obligacji, tym większe odnotowuje się wahania cen obligacji przy zmianie rentowności obligacji (przy założeniu, że są to obligacje o stałym oprocentowaniu, jednakowym oprocentowaniu i jednakowej rentowności na początku).

Podsumowując, im niższe oprocentowanie lub im dłuższy termin do wykupu obligacji, tym są one bardziej podatne na zmiany cen. Rozpatrzmy te właściwości na drugim przykładzie.

Przykład 2

Dane są dwie obligacje X i Y o stałym oprocentowaniu 5% i wartości nominalnej 1000 zł. Odsetki w obu przypadkach są wypłacane raz w roku. Termin wykupu obligacji X przypada za 1 rok, natomiast obligacji Y za 3 lata. Rentowność obu obligacji jest jednakowa i wynosi 5%, jednak w związku z przewidywanym wzrostem stóp procentowych oczekuje się wzrostu wymaganej stopy dochodu o 1 pkt procentowy. W jakim stopniu zmieni się kurs obligacji X oraz Y?

Zgodnie z naszymi wyliczeniami z poprzedniego przykładu, w aktualnej sytuacji rynkowej (tj. gdy oprocentowanie obligacji oraz YTM wynosi 5%) cena obligacji jest równa ich wartości nominalnej.

  1. obligacja X (po spadku YTM do 4%)
    wzór 4
  2. obligacja Y (po spadku YTM do 4%)
    wzór 5

Zgodnie z naszym założeniem, kurs obligacji, która posiadała dłuższy termin do wykupu zmniejszył się w znacznie większym stopniu.

Rozpatrzmy teraz te same obligacje X i Y, jednak przy założeniu, że mają taki sam termin wykupu (3 lata), ale różne oprocentowanie. Oprocentowanie obligacji X wynosi 4%, natomiast obligacji Y – 5%. Rentowność obligacji wynosi 5%. W jakim stopniu zmieni się kurs obu obligacji przy założeniu, że YTM obniży się o 1 pkt procentowy? 

  1. Cena obligacji X dla YTM = 5%
    wzór 6
    Cena obligacji X po spadku YTM do poziomu 4%

    wzór 7Procentowa zmiana ceny wyniosła 2,72%.

  2. Cena obligacji Y dla YTM = 5%
    wzór 8
    Cena obligacji X po spadku YTM do poziomu 4%
    wzór 9Procentowa zmiana ceny wyniosła 2,70%.

Zgodnie z naszym założeniem, kurs obligacji, która posiadała niższe oprocentowanie zmienił się w większym stopniu.

Z przedstawionych w powyższym artykule przykładów można wysnuć wniosek, że wahania kursów obligacji notowanych na Catalyst mogą następować w wyniku tych samych zdarzeń rynkowych, jednak często ten sam czynnik może w różnym stopniu wpłynąć na kurs obligacji. Należy o tym pamiętać zwłaszcza w przypadku, gdy mamy do czynienia z obligacjami o krótkim terminie do wykupu.

Autor: Tomasz Styrcula